The second exericse of the last episode features a fun little “Chrome-is-offline” game of the Project Zero team capturing bugs (and avoiding walls, I wonder if there’s an analogy there) at https://pzero-adventures-web.h4ck.ctfcompetition.com/.

Once the game is over, and your score is high enough, the website presents an option to be added to the high scores and then displays that page until refresh.

I looked at the network traffic after this process and found the following requests:

• POST to /api/sign with the parameters name and score. The response is some hex-encoded value.
• POST to /api/highscores with the parameters name, score, and signature. The response congratulates you on your place on the leaderboards.
• GET to /api/highscores, returning the high score list.

After quick testing, it seems that you are only able to be successfully added to the high scores with a valid signature. The server happily signs even very high scores, and there’s not much indication of what I should achieve here.

I then noticed that the challenge gives a hint:

Hint: Can you score lower than zero?

Testing it out, the server doesn’t agree to sign a negative score. Maybe it’s some overflow issue?

I also noticed that the challenge also graciously provides the entire source code of the website. It’s a pretty simple Flask server.

In app.py, we can see the endpoints available on the server. The endpoints I previously noticed were present. Looking at the code of the /api/highscores POST handler, the hint suggestion becomes evident:

if score < 0:
    # FIX(mystiz): I heard that some players are so strong that the score is overflown.
    #              I'll send them the flag and hope the players are satisfied for now...
    return {"message": f"You performed so well so that you triggered an integer overflow! This is your flag: {FLAG}"}

The handler takes name, score, and signature parameters, and it accepts a score smaller than 0 since the verification check is: if type(score) != int or not -2**16 <= score < 2**16.

However, after this verification and before the check on the negative score (and printing the flag), the handler calls verify(KEY_ID, name, score, signature) and exits on any exception.

Within verify, using the class VerifyingKey that verifies RSA signatures, the server checks that the signature of json.dumps([KEY_ID, name, score]) matches the given signature, where KEY_ID is a public RSA key it takes from a local file.

def verify(key_id, player_name, score, signature):
    with open(f'./keys/{key_id}.pub') as f:
        key_bytes = f.read()
    key = RSA.import_key(key_bytes)
    vk = VerifyingKey(key.n, key.e)
    message = json.dumps([key_id, player_name, score]).encode()
    return vk.verify(message, signature)

The signature, as I saw, is also given by the server too, through a different endpoint - a POST to /api/sign.

Inspecting its handler code, it takes the name and score parameters and signs them using the RSA private key that corresponds to the public key used to verify. However in this handler, the verification check on score is: if type(score) != int or score < 0.

So, I can freely sign a score that is any positive integer, but I somehow need to get a valid signature for a score that is a negative integer.

I tried and tested some ways to sneak in a negative integer to be signed.

It can’t be something with a large positive integer, as Python has no problem storing arbitrarily large integers. Also, I couldn’t really affect the signed string since the server signs json.dumps([KEY_ID, name, score]). So even though I control both name and score, I’m unable to affect one through the other - as an example using name="nam" and score=5 the signed message will be (the string) '["pzero-adventures", "nam", 5]'.

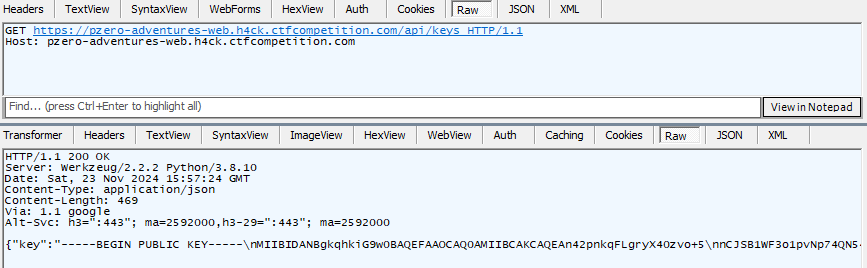
Feeling a little defeated, I suddenly noticed that the server also exposes an /api/keys endpoint, which simply responds with the server’s public key. At the point I knew - this has to be a cryptography challenge!

@app.route("/api/keys")
def get_key():
    with open(f'keys/{KEY_ID}.pub') as f:
        return {"key": f.read()}

Crypo challenges are notoriously hard - besides requiring a creative approach like other challenges, they also rely on a deep understanding of certain cryptography systems, involving pretty tough maths, techniques, and attacks.

Anyhow, with that realization, the main focus should be crypto.py which hosts the code used to sign and verify. The server doesn’t rely on a library for this (another sign alluding to a crypto challenge I missed earlier).

The file contains two classes, VerifyingKey and SigningKey used by util.py for the signing and verifying functionality.

Skimming over the SigningKey code, the plaintext signature is built using a standard signature notation for binary data called DER. The most important part of the structure is a hash (SHA256) of the message to be signed. For the last step, the plaintext signature is encrypted using the server’s private RSA key.

The VerifyingKey class, on the other hand, decrypts a given signature using the server’s public RSA key, verifies the DER format and structure, and then checks that the hash encoded within matches the hash of a given message, and if so, returns that the message is verified.

A comment on top of the sign and verify functions directed me to RFC2313, which describes a cryptographic system using RSA encryption. Specifically, it defines version 1.5 of PKCS#1 (Stands for “First Public-Key Cryptography Standard”).

This family of standards includes several primitives - encryption, description, signing, and verification.

A classic move with cryptography challenges you have no clue about (which was my situation) - you search for known attacks on the cryptosystem that is used here.

The search query: “PKCS #1 v1.5 attack” leads to multiple articles about a “Bleichenbacher attack”. That’s a good sign, and it’s time to do some reading.

This attack, published in 1998 by Daniel Bleichenbacher, enabled attackers to gradually reveal the content of an encrypted message in the PKCS #1 v1.5 format, by abusing the fact that many servers implementing decryption “leaked” whether the padding in the structure was correct or not.

This information is enough that, using about a few million queries (not much for a modern computer), the RSA private key could be reconstructed. And that’s how it is with cryptosystems - a seemingly tiny amount of information might be the flaw to brings the entire system down.

But what does this have to do with my case? We’re not dealing with the encryption-decryption part of the system, but rather with signing and verification.

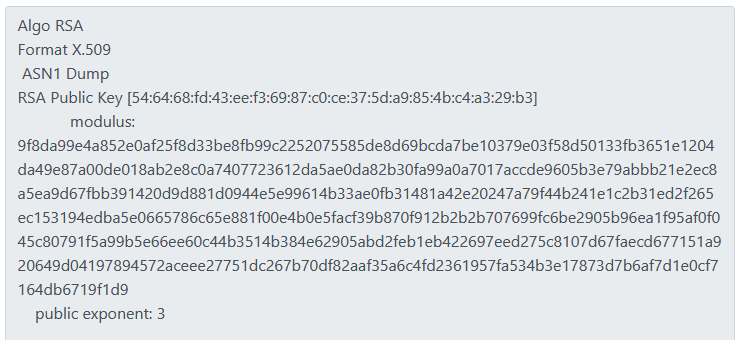
I found that in 2006, a variant of this attack was presented by Bleichenbacher, showed how, in cases where the RSA public key (e) is 3, it was possible to easily forge a fake signature.

Hey, that sounds like something more related, but is the public key 3 here? I quickly queried the server at api/keys which revealed that the server’s public key is indeed 3!

(As a side note, you may ask if this is even reasonable for a “real life” attack? Well, back then it was very common to use 3 as the public key since it doesn’t matter for the key generation algorithm, while really matters for the speed of using the key - having to multiply a number just 3 times makes the encryption and verification very quick!)

So, it’s pretty clear I need to implement Bleichenbacher’s attack. But how it works? Actually, the signing attack (compared to the decryption version) is not too complicated.

Starting with a tl;dr for the attack: Bleichenbacher exploited the fact that many verifiers, after decrypting the signature only check that it starts with the correct 2-byte header, skip over the padding, and parse the following bytes as the signature.

By skipping over the padding and not checking that it indeed pads properly, attackers could send signatures with short padding, which in turn made verifiers essentially only look at a small prefix of the plaintext signature. When the public key is small, we can quite easily forge signatures beginning with whatever we desire.

Let’s see this! Starting off, we know that the RSA public key (e) is 3.

The signature verification function starts by taking an encrypted signature and decrypting it. In an RSA system, it means raising the signature (in integer form) to the power of the public key and calculating the result modulo the modulus n (= dividing by n and taking the remainder).

So for our public key, the verification function receives an encrypted signature and just raises it to the 3rd power (AKA cubing it).

k = pow(s, self.e, self.n) # s is the signature, e is the public key, n is the modulus

In case the encrypted signature s is a small integer (less than the cube root of n), then the result of this operation will be smaller than n, meaning no modulus operation happens. If the verifier only cares about the beginning of the plaintext signature, this behavior is risky.

Why? Theoretically, if we want this decryption operation to output a certain signature, we can start from the signature in its integer form and simply take its cube root, then pass it to the verification function as the encrypted signature.

This obviously won’t always work - since we’re working with whole integers, the chances our signature’s cube root is an exact integer are very very very small.

However, if we just round the root cube result to the next integer, then the cube of that integer won’t be too far from the number we started from - meaning that some prefix of it won’t be affected!

This can be easily shown via an example: let’s imagine we’re working with 8-digit decimal integers, and we want our signature to start with 17.

We take the number 17,000,000 and take its cube root. We get the number 257.128159.... Taking the next integer (258) as the “encrypted signature”, its cube is 17,173,512. As you can see, the desired prefix is retained! We only had to incur a bunch of random numbers after it.

So we have the “ability” to forge signatures with a determined prefix using Bleichenbacher’s attack, how can it help me win the challenge?

It’s time to take a look at the form of a PKCS#1 v1.5 signature:

0x00 # Separator
0x01 # Block type for signature
0xFF 0xFF ... 0xFF # Padding to make the signature exactly 256 bytes long
0x00 # Separator
0x30 # Outer DerSequence Start 
0x31 # Outer DerSequence Length - 0x31
0x30 # Inner DerSequence Start
0x0d # Inner DerSequence Length - 0x0D
0x06 # AlgorithmObjectId Start
0x09 # AlgorithmObjectId Length - 0x09
0x608648016503040201 # AlgorithmObjectId - '2.16.840.1.101.3.4.2.1'
0x05 # Null Start
0x00 # Null Length - 0x00
0x04 # OctetStringHash Start
0x20 # OctetStringHash Length - 0x20
0xef2d... # OctetStringHash - SHA256 of the message to be signed

Or, more succinctly:

00 01 | Padding | 00 | DerSequence(DerSequence(AlgorithmObjectId, Null), OctetStringHash)

As I mentioned above, after decrypting the signature, verifiers didn’t bother checking that the padding really is large enough to pad the entire signature to be 256 characters long.

Instead, they separated the signature on the null bytes (0x00), verified the minimum amount of padding (8 bytes), and then moved on to parse the signature. If we count the number of bytes of such a “short” version of a signature, we have:

2 (Header bytes) + 8 (Padding) + 1 (Separator) + 0x33 (DerSequence: 0x31 + Header: 2)

For a total of 62 bytes, leaving 256-62=194 bytes remaining as the signature suffix, the “prefix attack” is very feasible!

Glancing quickly at the verify function the server uses:

def verify(self, m, s):
    if len(s) != self.bits//8:
        raise Exception('incorrect signature length')
    s = int.from_bytes(s, 'big')

    k = pow(s, self.e, self.n)
    k = int.to_bytes(k, self.bits//8, 'big')
    if k[0] != 0x00:
        raise Exception('incorrect prefix')
    if k[1] != 0x01:
        raise Exception('incorrect prefix')
    
    padding, digest_info = k[2:].split(b'\x00', 1)

    if len(padding) < 8:
        raise Exception('invalid padding length')
    if padding != b'\xff'*len(padding):
        raise Exception('invalid padding content')

    sequence = DerSequence()
    sequence.decode(digest_info)
    _digest_algorithm_identifier, _digest = sequence

    sequence = DerSequence()
    sequence.decode(_digest_algorithm_identifier)
    _digest_algorithm_identifier = sequence[0]

    object_id = DerObjectId()
    object_id.decode(_digest_algorithm_identifier)
    digest_algorithm_identifier = object_id.value
    if digest_algorithm_identifier != '2.16.840.1.101.3.4.2.1':
        raise Exception('invalid digest algorithm identifier')

    _null = sequence[1]
    null = DerNull()
    null.decode(_null)

    octet_string = DerOctetString()
    octet_string.decode(_digest)
    digest = octet_string.payload

    if hashlib.sha256(m).digest() != digest:
        raise Exception('mismatch digest')
    return True

Notice this part in particular:

padding, digest_info = k[2:].split(b'\x00', 1)

if len(padding) < 8:
    raise Exception('invalid padding length')

It seems the server is susceptible to this attack! Let’s implement it:

import hashlib
import json

from Crypto.Util.asn1 import DerSequence, DerObjectId, DerOctetString, DerNull
from Crypto.PublicKey import RSA
from gmpy2 import mpz, root

KEY_ID = 'pzero-adventures'

def forge_signature(message):
    with open(f'{KEY_ID}.pub') as f:
        key_bytes = f.read()
    key = RSA.import_key(key_bytes)
    n = key.n

    digest = hashlib.sha256(message).digest()
    digest_algorithm_identifier = DerSequence([
        DerObjectId('2.16.840.1.101.3.4.2.1').encode(),
        DerNull().encode()
    ])
    digest_info = DerSequence(([
        digest_algorithm_identifier,
        DerOctetString(digest).encode()
    ]))

    # Creating the 62-byte prefix we need
    # 00 01 | FF FF FF FF FF FF FF FF | 00 | DerSequence(AlgorithmObjectId, Null, OctetStringHash)
    plaintext_prefix = b"\x00" + b"\x01" + b"\xFF" * 8 + b'\x00' + digest_info.encode()
    
    # Plaintext needs to be exactly the size of n
    remaining_plaintext_length_bytes = n.bit_length() // 8 - len(plaintext_prefix)
    # So we'll pad the prefix with 0s up to the required length.
    plaintext = plaintext_prefix + b"\x00" * remaining_plaintext_length_bytes
    plaintext_as_int = int.from_bytes(plaintext, 'big')

    # Rounding up the cube root to keep the prefix intact
    signature_as_int = int(iroot(mpz(plaintext_as_int), 3)[0]) + 1

    # Verifying the signature prefix matches the required plaintext
    decrypted_signature_int = pow(signature_as_int, key.e, key.n)
    decrypted_signature = int.to_bytes(decrypted_signature_int, n.bit_length() // 8, 'big')
    assert(decrypted_signature.startswith(plaintext_prefix))

    return signature_as_int

forge_signature(json.dumps([KEY_ID, "nam", -1]).encode())

Executing the code and the assertion at the end passes successfully!

Out of interest, I looked at the parts of this attack.

Here’s the required prefix (as hex):

0x0001ffffffffffffffff003031300d060960864801650304020105000420707eca926424f185c834f219d311950df8bdfa8a83fc2e3b36e6c2210450853e

Here’s the encrypted signature (as an integer)

0x995391042663285905082373840334783075535901580439276937985819219650252243000986193655522714919094035649842008832283737311056527766480523975681564515126086150333565353700999252276489952678424776872790802557

And here’s the decrypted signature (taking the cube of the previous integer)

0x0001ffffffffffffffff003031300d060960864801650304020105000420707eca926424f185c834f219d311950df8bdfa8a83fc2e3b36e6c2210450853e0000000000000000000000000000000000000000000000001c81eb218cbb1ab79b2b50f867c81eac3df9df425878772c2303ed2ac4a9142b857696bd8aa8da0875473d69710885526d8500b31b825a066944156a249a4683d3d610d104d92b69e8fb0f385dae55a42e1490205251f682ee9d1427b4275f322ef5fcbdf5257bcfca8f8469417d0f182006a01ffff2ce8a3e04d16c008cd53afbc65a48a591e334e926b10012cd0842bf4c2ccfc4bb699d4de92b50a24789b57f92125d381dbe118d65

-->
# Prefix
0x00 0x01 
# Padding
0xffffffffffffffff 
# Separator
0x00 
# Outer DerSequence
0x30 0x31 
# Inner DerSequence
0x30 0x0d 
# AlgorithmObjectId
0x06 0x09 0x608648016503040201 
# Null
0x05 0x00 
# OctetStringHash
0x04 0x20 0x707eca926424f185c834f219d311950df8bdfa8a83fc2e3b36e6c2210450853e 
# Garbage suffix
0x0000000000000000000000000000000000000000000000001c81eb218cbb1ab79b2b50f867c81eac3df9df425878772c2303ed2ac4a9142b857696bd8aa8da0875473d69710885526d8500b31b825a066944156a249a4683d3d610d104d92b69e8fb0f385dae55a42e1490205251f682ee9d1427b4275f322ef5fcbdf5257bcfca8f8469417d0f182006a01ffff2ce8a3e04d16c008cd53afbc65a48a591e334e926b10012cd0842bf4c2ccfc4bb699d4de92b50a24789b57f92125d381dbe118d65 

As can be easily seen, it starts with the prefix I wanted, and there are even multiple extra null bytes to spare after the OctetStringHash is over!

I spun a local version of the server and sent the signature to the server, and it worked! Kinda’…

This signature passes the padding check, but when the code executes sequence = DerSequence(); sequence.decode(digest_info), it crashes with an error: ValueError: Unexpected extra data after the DER structure

The digest_info variable holds a string that starts with a correct DER structure but ends with garbage. Unfortunately, the Python implementation of DerSequence doesn’t really care the reported length is 0x31, and won’t peacefully accept the garbage.

This could’ve been the solution if the split on the null byte (padding, digest_info = k[2:].split(b'\x00', 1)) wouldn’t have stopped after the first one, but unfortunately, this doesn’t seem like the end of the challenge.

I need to somehow make it so the decoding of the DerSequence works with the suffix garbage…

Ah, I could increase the prefix just a little bit, and make the outer DerSequence include yet another object and look something like that:

DerSequence(DerSequence(AlgorithmObjectId, Null), OctetStringHash, OctetStringGarbage)

To declare another OctetString, I only need to write down 04 after the OctetStringHash followed by the length of the rest of the garbage, which would be encoded as 81 BF. I easily have 3 bytes to spare.

However, I noticed the parsing code would still fail, since the line _digest_algorithm_identifier, _digest = sequence only unpacks 2 values from the sequence, and not 3.

Well, this idea could work if I instead put the garbage in the first inner DerSequence, so the outer DerSequence would look like this:

DerSequence(DerSequence(AlgorithmObjectId, Null, OctetStringGarbage), OctetStringHash)

Then the unpacking would work! Also, the code only looks at the first object from the inner sequence DerSequence.

However, this way won’t allow using Bleichenbacher’s “prefix attack” - my signature would need to end with the hash, which would be overwritten by the prefix attack.

I wondered if someone had already bumped into this issue in the past. Online, I bumped into this neat article from 2016 by Filippo Valsorda, who discovered the python-rsa module is vulnerable to signature forgery.

The verification code was not vulnerable to Bleichenbacher’s “prefix attack”, but rather the issue was that it didn’t validate that the padding bytes are actually composed of 0xFF, so Filippo’s idea was to hide the garbage in the padding, leading him to the same issue of having including the OctetStringHash object at the end of the signature!

The server code does not have this padding issue, since it verifies that:

if padding != b'\xff'*len(padding):
    raise Exception('invalid padding content')

So, while not exactly the case I have here, if I learn how Filippo managed to have the required OctetStringHash suffix in the final signature, I can still hide the garbage in the inner DerSequence.

After reading the article, I can honestly say that the trick is nothing short of magic. And although it’s explained really well, I’ll give it a shot here too.

We’re going to start with smartly crafting a suffix of the encrypted signature, which when cubed results in the required plaintext suffix (the hash).

Then, we do the same “prefix trick” as before to find an encrypted signature that when cubed, results in a plaintext starting with the required prefix.

The theory is that if we simply replace the last bytes of this encrypted signature with the encrypted signature suffix we just found, nothing will happen to the prefix after decryption!

This is because the suffix is so small (the OctetStringHash is just 34 bytes), so changing that part of the encrypted signature shouldn’t affect the prefix which “hides” in the high bytes of the signature.

Again, I’ll show how this works with a practical example: let’s say we want our signature to end with 0x40000000. Taking a cube root, our encrypted signature suffix should be 0x400.

Before, when we constructed the encrypted signature with a chosen prefix, we ended up with the following:

prefix_sig = 995391042663285905082373840334783075535901580439276937985819219650252243000986193655522714919094035649842008832283737311056527766480523975681564515126086150333565353700999252276489952678424776872790802557

Let’s convert it to bytes and replace its suffix with 0x400:

new_sig = int.from_bytes(
              bytes.fromhex(prefix_sig.to_bytes(256, 'big').hex()[:-3] + '400'),
              'big')

Now, if we decrypt the new signature:

print(binascii.hexlify(pow(new_sig, 3).to_bytes(2048//8, 'big')))

We get:

0x0001ffffffffffffffff003031300d060960864801650304020105000420707eca926424f185c834f219d311950df8bdfa8a83fc2e3b36e6c2210450853e00000000000000000000000000000000000000000000006a4c9066ab2297aeca29a48c5dd52a13fa1f6cf11b14e87dbf36ca2248193084cd1b1dcd5e5684e25544a970142eb7a8a57953aff65f7399343df9ff7a843cdd8d70848ee6c06fef71c5e70c9b82077bdf2da1b86d2db93c817e57bf971393cb0007e0f06f24e3512e78ef845aa5c3f5231a504be11a2b4350c182bae410d7096f78c34a73136f660ee491d241e9d0606fa24992268502a1711691962bd042118fdf7a4cd05b1c40000000

As you can see, we have the suffix we wanted (0x40000000), and the prefix is still intact!

(<note>

In some cases, depending on the exact suffix, the conversion might “carry” a bit over and so the last bit of the prefix will change as well as the null bytes become a bunch of 0xFF bytes.

To avoid this, we’ll pad the required prefix with random values instead of null bytes:

def forge_signature(message):
    # ...
    
    # Plaintext needs to be exactly the size of n
    remaining_plaintext_length_bytes = n.bit_length() // 8 - len(plaintext_prefix)
    # So we'll pad the prefix with random bytes up to the required length.
    plaintext = plaintext_prefix + os.urandom(remaining_plaintext_length_bytes)

    # ...
    return signature_as_int

print(forge_signature(json.dumps([KEY_ID, "name", -1]).encode()))

</note>)

So now we know how this “suffix magic trick” works.

But, did you notice I cheated? I chose a suffix with a perfect integer cube root. So given an arbitrary suffix (whose cube root is not an integer), how can we find its corresponding encrypted suffix?

Since it doesn’t have a perfect cube root, we’ll find a longer suffix with an integer cube root that ends with the required suffix. Does that sound difficult? Apparently not! It only takes a simple iterative process that slowly discovers the required encrypted signature suffix and works as follows:

We start with 1 as the encrypted signature suffix. The iterative process takes the current encrypted signature suffix, cubes it, and sees which bits of the output match the required signature suffix, going from least significant to most significant bits.

When we bump into a mismatch at some index, we flip the bit at this index in the encrypted signature suffix.

This has a twofold effect: the cube’s bit also flips, meaning now this index matches. Additionally, since cubing is basically a bunch of multiplications, changing the bit at some bit index doesn’t affect the output bits that are less significant to this bit (recall long multiplication from school - the later rows in the intermediary result were shifted to the left, making it so they don’t affect previous indices).

Eventually, this process either reaches a point where the resulting cubed signature suffix contains the required suffix, which means we won, or otherwise, the constructed encrypted signature suffix grows so large its cube is larger than n, meaning the process has failed.

But since our required suffix is so small relative to n, we’re basically promised it will succeed. Filippo has a nice diagram showing this with a practical example:

Let’s imagine our required suffix is 0b1010101101. Here’s the iterative process:

1.
encrypted_sig_suffix:   0000000001
cubed_suffix:           0000000001
required_suffix:        1010101101

The 2nd bit doesn't match. We'll flip it.

2. 
encrypted_sig_suffix:   0000000101
cubed_suffix:           0001111101
required_suffix:        1010101101

The 4th bit doesn't match. We'll flip it.

3. 
encrypted_sig_suffix:   0000010101
cubed_suffix:        ...0000101101
required_suffix:        1010101101

The 7th bit doesn't match. We'll flip it.

4. 
encrypted_sig_suffix:   0010010101
cubed_suffix:        ...0110101101
required_suffix:        1010101101

The 8th bit doesn't match. We'll flip it.

5. 
encrypted_sig_suffix:   0110010101
cubed_suffix:        ...0010101101
required_suffix:        1010101101

The 9th bit doesn't match. We'll flip it.

6. 
encrypted_sig_suffix:   1010010101
cubed_suffix:        ...1010101101
required_suffix:        1010101101

Success!

The final encrypted signature suffix is 0b1010010101. Its decrypted version ends with 1010101101 prepended with some bits we don’t care about.

With this method to generate the encrypted signature suffix, I can do Bleichenbacher’s “prefix trick”, then simply replace the suffix of the result.

On the prefix side, since the suffix is so small compared to the entire signature, replacing the suffix won’t affect the prefix (but rather the junk bytes between them)

On the suffix side, since it is inserted as a suffix to a larger integer, the more significant bits won’t affect the decrypted version of this suffix, the same as what we exploited in the iterative process.

One note is that the plaintext signature has to start with 1 (due to the iterative process starting with 1). This means we can only aim for odd suffixes. However since the hash is a SHA256 of a value we control (the name), we can easily manually find a value that results in an odd hash.

Before sitting down to write the code, however, I needed to know what the updated prefix should be. If you recall, I’m trying to construct the following signature:

00 01 | FF FF FF FF FF FF FF FF | 00 | DerSequence(DerSequence(AlgorithmObjectId, Null, OctetStringGarbage), OctetStringHash)

I need to calculate the amount of garbage we’re going to have. The signature header, padding, and separator are 11 bytes, the hash is 32 bytes, the algorithm object is 9 bytes, and, DER headers account for 15 more bytes. So the remaining 189 bytes will be the garbage.

Summarizing, the signature will look as follows:

0x00 0x01 # Prefix
0xFFFFFFFFFFFFFFFF # Padding
0x00 # Separator
0x30 0x81 0xF2 # Outer DerSequence
0x30 0x81 0xCD # Inner DerSequence
0x06 0x09 0x608648016503040201 # AlgorithmObjectId
0x05 0x00 # Null
0x04 0x81 0xBD {GARBAGE}
0x04 0x20 {HASH} # OctetStringHash

This dictates the necessary required prefix and suffix. It’s time to write some code!

def forge_signature_2(message):
    with open(f'{KEY_ID}.pub') as f:
        key_bytes = f.read()
    key = RSA.import_key(key_bytes)

    digest = hashlib.sha256(message).digest()

    # Required suffix - DerSequence of the hash
    plaintext_suffix = b'\x04\x20' + digest # OctetString - type 0x04, length 0x20
    assert(plaintext_suffix[-1] & 1 == 1) # Verify that the suffix is odd
    plaintext_suffix_int = int.from_bytes(plaintext_suffix, 'big')

    def bit_at(integer, index):
        return ((1 << index) & integer) >> index
    
    # Iterative process to find an encrypted signature suffix
    encrypted_signature_suffix_int = 1
    for bit in range(len(plaintext_suffix) * 8):
        # If the decryption of the current candidate doesn't match the suffix
        if bit_at(encrypted_signature_suffix_int ** 3, bit) != bit_at(plaintext_suffix_int, bit):
            # Set the bit to 1
            encrypted_signature_suffix_int = (1 << bit) | encrypted_signature_suffix_int 
    
    # Verify that the resulting encrypted signature ends with the suffix
    assert(int.to_bytes(encrypted_signature_suffix_int ** 3, key.n.bit_length() // 8, 'big').endswith(plaintext_suffix))

    encrypted_signature_suffix = int.to_bytes(encrypted_signature_suffix_int, (encrypted_signature_suffix_int.bit_length() + 7) // 8, 'big')

    # Required prefix
    plaintext_prefix = b'\x00\x01' + b'\xFF' * 8 + b'\x00'
    plaintext_prefix += b'\x30\x81\xF2' # Outer DerSequence - type 0x30, length 0xF2
    plaintext_prefix += b'\x30\x81\xCD' # Inner DerSequence - type 0x30, length 0xCD
    plaintext_prefix += b'\x06\x09\x60\x86\x48\x01\x65\x03\x04\x02\x01' # AlgorithmObjectId - type 0x06, length 0x09
    plaintext_prefix += b'\x05\x00' # Null - type 0x05, length 0x00
    plaintext_prefix += b'\x04\x81\xBD' # OctetString - type x04, length 0xBD

    # Verify sizes of prefix, garbage, and suffix match the needed signature length
    assert(len(plaintext_prefix) + 0xBD + len(plaintext_suffix) == key.n.bit_length() // 8)

    # Construct the encrypted signature with the prefix
    remaining_plaintext_length_bytes = key.n.bit_length() // 8 - len(plaintext_prefix)
    padded_plaintext_prefix = plaintext_prefix + os.urandom(remaining_plaintext_length_bytes)
    padded_plaintext_prefix_int = int.from_bytes(padded_plaintext_prefix, 'big')
    encrypted_signature_prefix_int = int(iroot(mpz(padded_plaintext_prefix_int), 3)[0]) + 1

    # Verify that the resulting encrypted signature starts with the prefix
    assert(int.to_bytes(encrypted_signature_prefix_int ** 3, key.n.bit_length() // 8, 'big').startswith(plaintext_prefix))

    # Replace the end of the encrypted signature prefix with the encrypted signature suffix
    encrypted_signature_prefix = int.to_bytes(encrypted_signature_prefix_int, key.n.bit_length() // 8, 'big')
    encrypted_signature = encrypted_signature_prefix[:-len(encrypted_signature_suffix)] + encrypted_signature_suffix

    encrypted_signature_int = int.from_bytes(encrypted_signature, 'big')

    return encrypted_signature_int

signature = int.to_bytes(forge_signature_2(json.dumps([KEY_ID, "tes", -1]).encode()), 2048 // 8, 'big')
verify(KEY_ID, "tes", -1, signature)

Executing the above with the previous name and score ("nam", -1) resulted in an even hash. I switched it to "tes", -1 and the code works flawlessly! Passing it through a local version of verify, it returns True!

Here are the required prefix and the suffix (as hex strings):

0x0001ffffffffffffffff003081f23081cd060960864801650304020105000481bd # Prefix
0x04205c354e41c261f1f569f1762a999ab8ae7250d742c41075c7f33b4d776f574d55 # Suffix

And here’s the resulting signature’s decryption:

0x0001ffffffffffffffff003081f23081cd060960864801650304020105000481bdf0ae420ff8a06a85259b02a6791f05b9e66684caad51d6b5d8525e4f841c3fd675ebe8d2f67e0e953fbc2830e217417abc73f93194ecba3452585b7d42f128964b6b48187ceaf663f831a4e9a9bc969964d914e36241724622d97c7abffeb70431fdee61a3bc2e832c8b0e016792bf6b2f434f2911ed2d579c77e0a8d0315767bc17d3f8887f99adaf9de8c4ba6958140681e9e8c3837a18a3b3fc047bd738219653ca87631acbc9a5de490f1e9744c415bbbaa075a1715b200903a22704205c354e41c261f1f569f1762a999ab8ae7250d742c41075c7f33b4d776f574d55

It begins with the prefix and ends with the suffix, huge success!. Sending the signature as a 256-byte long hex string to the server…

HTTP/1.1 200 OK
Server: Werkzeug/2.2.2 Python/3.8.10
Date: Fri, 04 Oct 2024 13:37:34 GMT
Content-Type: application/json
Content-Length: 166
Via: 1.1 google
Alt-Svc: h3=":443"; ma=2592000,h3-29=":443"; ma=2592000

{"message":"You performed so well so that you triggered an integer overflow! This is your flag: 

Thanks Bleichenbacher and Filippo! :)

As a final note, this was one of the first cryptography challenges I managed to solve. In previous CTFs, I mostly ignored them assuming I’m unlikely to solve them. I guess one takeaway is that the attacks explored in these challenges are quite well documented, and with time the more knowledge you gather on a specific type of cryptographic system and common attacks, the easier and faster it is to solve CTF challenges around it.